Astronomia x Astrologia

Pironautas, vi esse vídeo sensacional do canal Nerdologia e tive que compartilhar. Excelente comparação entre astronomia e astrologia. Crédito ao Átila e ao Jovem Nerd.

Matemática e Música - Um passeio numérico através dos sons

"A música é uma ciência que necessita possuir um estatuto definido. Suas regras devem ser extraídas de um princípio claro, inconcebível sem o auxilio da matemática. Apesar de toda a experiência que eu posa ter em música por associar-me a ela por tanto tempo, devo confessar que somente com auxílio ma matemática, minhas idéias tornaram-se claras e a luz substituiu uma escuridão da qual eu não estava ciente." 

              Rameau, 1722


     A relação entre a música e a matemática é muita antiga. Na Grécia antiga, com as experiências de sábios como Pitágoras e Arquitas, até os séculos XVIII, com cientistas musicais tais como Saveur, Rameau, Daniel Bernoulli, Euler, Ohm, Fourier e Helmholtz, fortes contribuintes na explicação racional de fenômenos matemático-musicais como o Temperamento e Séries Harmônicas. Embora essa relação provavelmente fosse conhecida superficialmente antes dos pitagóricos, estes foram os primeiros a registrar e explorar essa relação. Os pitagóricos foram os únicos até Aristóteles a fundamentar cientificamente a música, começando  a desenvolvê-la e tornando-se aqueles mais preocupados por este assunto. Como principais teóricos musicais dessa escola são Pitágoras e Filolaus no período pré-clássico e Arquitas, Aristoxeno e Aristóteles no período clássico.
     Provavelmente inventado por Pitágoras, o monocórdio é um instrumento composto por uma única corda (berimbau???) estendida entre dois cavaletes fixos sobre uma prancha ou mesa possuindo ainda um cavalete móvel colocado sob a corda para dividi-la em dois. A princípio, seus experimentos evidenciavam relações entre comprimento da corda estendida e a altura musical do som emitido quando tocada (não confundir altura musical com altura do volume - altura musical é a variação entre altura dos sons graves, com frequência baixa e sons agudos, com frequência alta; e altura de volume é a variação da amplitude da onda, variando entre volume baixo e volume alto). Pitágoras buscava relações de comprimentos - razões de números inteiros - que produzissem determinados intervalos sonoros. Em seu experimento, observou que pressionando um ponto situado a 3/4 do comprimento da corda em relação a sua extremidade e tocando a corda ouvia-se uma quarta acima do tom emitido pela corda inteira. Analogamente, exercida a pressão a 2/3 do tamanho ouvia-se uma quinta acima e a 1/2 obitinha-se a oitava do som original.
     A descoberta da relação entre razão de números inteiros (1/2, 2/3 e 3/4) e tons musicais mostrou-se significativa naquela ocasião, gerando uma dúvida fundamental para o pensador de Samos: Por que as consonâncias musicais subjazem razões de pequenos números inteiros? Qual a causa e qual o efeito? Pitágoras justificou a subjacência de pequenos números inteiros às consonâncias pelo fato de que os números 1, 2, 3 e 4, envolvidos nas frações mencionadas, geravam toda a perfeição. Os pitagóricos consideravam o número quatro (primeiro quadrado par) origem de todo o universo, representando a matéria em quatro elementos. Com essas razões, poderíamos por exemplo, partindo de um fá e subindo uma quinta (2/3) obteremos um dó, que por sua vez subindo outra quinta teremos um sol, repetindo teremos um ré (oitava acima), seguido de lá, mi e si, formando a sequência fá, dó, sol, ré, lá, mi e si, e remanejando apresenta-se dó, ré, mi, fá sol, lá e si. Tal relação de comprimentos 2/3 chama-se gama pitagórica. Assim obtém-se as relações 8/9 com ré, 16/27 com lá, 64/81 com mi e 128/243 com si, formando os intervalos de tom, tom, semitom, tom, tom, tom e semitom temperados. Partindo da nota dó e construindo a escala pelo percurso de quintas, o ciclos fecha-se formando a sequência dó, sol, ré, lá, mi, si, fá#, dó#, sol#, ré#, lá#, fá e dó. Porém estas notas correspondem, na gama temperada, a aproximações dos sons de fato alcançados.
     Um dos mais importantes teóricos musicais do período clássico, Arquitas de Tarento (430-360 a.C.) colaborou de maneira significativa não somente para o desenvolvimento da música mas para o desvendar de seus fundamentos racionais. Escreveu trabalhos científicos relacionados ao cálculos de intervalos musicais e proporções musicais. Entre suas contribuições, há evidências que possivelmente modificou a antiga denominação da média subcontrária para média harmônica, provavelmente pelo fato do comprimento relativo ao intervalo de quinta (2/3), de grande valor harmônico para os gregos, ser a média subcontrária entre o comprimento da corda solta e aquele correspondente à oitava, intervalo consonante fundamental. Arquitas também foi o primeiro pensador a associar altura musical à frequência pela comparação de sons emitidos por ventos fortes e fracos e deslocando o foco de atenções da fonte de emissão de som para o ar, antecipando em 2000 anos o estudo da Acústica (propriedades física do som) por parte de Galileu no séc. XVII.
     O renascimento teve um profundo papel no estudo da Música com ciência, seguido de alguns aprofundamentos importantes neste período na compreensão das idéias de Série Harmônica e Temperamento. Na parte musical o Renascimento caracteriza-se pela evolução da polifonia - superposição de melodias - e consequentemente desenvolvimento da harmonia. Caracterizada por processos de matematização, experimentação e mecanização, a Revolução Científica nos séc XVI e XVII propiciou a emergência de interpretações e argumentações inovadoras. Realizando trabalhos matemáticos concernentes a esta área em seu tratado Música Teórica, Ludovico Fogliane (1470-1539) forneceu subsídios para que Gioseffe Zarlino (1517-1590) organizasse em sua obra Inztituzioni Armonique (1558) a base científico-cultural em toda Europa durante dois séculos. Modificando substancialmente a concepção pitagórica, Galileu Galilei escreveu em 1638 que nem o comprimento, nem a tensão e nem a densidade linear de cordas apresentava-se como razão direta e imediata subjacente a intervalos musicais, mas razões dos números de vibrações e impactos de ondas sonoras que atingiam o tímpano. Considerando o som que alcaçava o ouvido invés do objeto vibrante que produzia, Galileu verificou que a altura musical relacionava-se diretamente à frequência registrando rastros de arranhões desenhados numa placa metálica provenientes de uma haste vibrante solidária a uma membrana que recebia vibrações sonoras. A percepção por parte de Galileu no séc. XVII de que a sensação de altura musical relaciona-se diretamente ao conceito de frequência marca o início da física da música em sua concepção atual.
     O padre e matemático francês Marin Mersenne (1588-1648) que apresenta-se como primeiro teórico a fundamentar o estudo de harmonia no fenômeno da ressonância. Trocando correpondência assídua com René Descartes (1596-1650) Mersenne discutiu problemas e aspectos pouco claros do Compendium Musicae escrito pelo filósofo francês em 1618.Constatando a possibilidade de acompanhar visualmente  os movimentos vibratórios das cordas, o matemática francês utilizava o próprio pulso com intuito de marcar o tempo necessário para completar um determinado número de ciclos. Variando os comprimentos e tensões, Mersenne verificou empiricamente que para frequências visualizáveis, a vibração de um fio esticado era inversamente proporcional ao comprimento da corda se sua tensão fosse constante; diretamente proporcional à raiz quadrada da tensão  se o comprimento fosse constante e inversamente  proporcional à raiz quadrada da massa por unidade de comprimento, para fios diferentes de mesmo comprimento e tensão, chegando na fórmula descrita:
onde f é a frequência, l o comprimento da corda, n uma constante inteira, T a tensão que a corda encontra-se sujeita e p a densidade linear da corda. A partir de tal descoberta, a natureza das consonâncias é retomada à luz das leis de corpos vibrantes. A fórmula citada implica em reorganizações de Mersenne a respeito de médias harmônicas e aritméticas em música. Para o matemático francês, a média aritmética possuía caráter superior à harmônica, pois tomando números proporcionais às vibrações - causas primeiras do som - a quinta na posição inferior resultava na média aritmética dos números que caracterizam a oitava.
     O matemático, astrônomo e filósofo nascido em Wiel, Johannes Kepler (1571-1630) apresentou, além de preciosos legados em física tais como as leis dos movimentos dos planetas, fortes subsídios para a ciência musical. Com o falecimento de Tycho Brahe em 1601, Kepler assumiu seu posto trabalhando na organização de calendários e na predição de eclipses como matemático e astrônomo da corte do imperador Rudolfo II em Praga até 1612, estabelecendo-se mais tarde em Linz, onde concluiu e publicou seu Harmonices Mundi em 1619. Principal contribuição do astrônomo alemão à teoria musical, essa obra compõe-se de 5 livros - os dois primeiros relacionam a origem das 7 harmonias com arquétipos inerentes à geometria e à Deus; o livro 3 apresenta um tratado sobre consonância e dissonância, intervalos, modos, melodia e notação; o livro 4 discorre sobre astrologia enquanto o volume 5 aborda a Harmonia das Esferas. O cientista alemão verificou empiricamente a existência de oito consonâncias: uníssono (1/1), oitava (1/2), quinta (2/3), quarta (3/4), terça maior (4/5), terça menor (5/6), sexta maior (3/5) e sexta menor (5/8). Dentre suas contribuições em música, Kepler defendia a existência de escalas musicais peculiares a cada planeta, que soavam como se estes cantassem simples melodias, relacionando para isso velocidades dos planetas às frequências emitidas.
     O compositor e teórico francês, Jean Philippe Rameau (1683-1764) iniciou seus estudos com seu pai que era organista profissional, frequentando durante a infância uma escola de jesuítas e cumprindo mais tarde um pequeno período de estudos na Itália. Em 1702, tornou-se maitre de musique da Catedral de Avignon, transferindo-se nesse mesmo ano para Catedral de Clermont e tornando-se em 1706 organista do colégio jesuíta em Paris. Em 1722, supervisionou a publicação do seu Traité de l'Harmonie, obra em que apresenta uma nova teoria sobre relação entre o baixo e a harmonia, baseada em suas concepções das propriedades físicas do som.
     O Traité de l'Harmonie compõe-se de 4 livros. O primeiro discorre sobre a relação entre relações harmônicas e proporções, o segundo  trata da natureza e propriedades dos acordes e tudo que pode ser utilizado para se atingir a música perfeita, o terceiro e quarto livros estabelecem respectivamente  princípios para composição e acompanhamento musicais. Somente o primeiro livro possui uma abordagem da música à luz da ciência. Segundo Rameau, a música é a ciência dos sons, portanto o som é principal matéria da música. Dividindo esta arte/ciência em harmonia e melodia, o teórico francês subordinou esta última à primeira, admitindo  que o conhecimento de harmonia é suficiente para a compreensão completa das propriedades da música. Estabelecendo uma relação biunívoca entre som e tamanho da corda, o teórico afirmou que cada corda contém em si mesma todas as outras menores que elas, mas não aquelas que são maiores; portanto os sons agudos estão contidos em sons graves, porém os sons graves não estão contidos nos agudos.
     Assim como Zarlino e Descartes, Rameau obteve os intervalos consonantes dividindo a corda em até 6 partes, afirmando que às consonâncias, subjaziam números consecutivos e que a ordem de tais números determinava a ordem e perfeição  das consonâncias. Segundo tal critério, a oitava - 1:2 possuia caráter mais consonante que a quinta - 2:3 - que por sua vez, apresentava-se mais consonante que a quarta - 3:4 - e assim por diante. Esta afirmação de Rameau mostrava-se ineficaz, uma vez que a sexta maior - 3:5 - além de não ser produzida por números consecutivos, não precedia a terça maior - 4:5 - nem a terça menor - 5:6.

     Segue abaixo a tabela dos intervalos músicais e as razões matemáticas:

Intervalo                 - Razão        - Nota (considerando Dó como a corda inteira)
Primeira justa         - 1 Corda     - Dó
Segunda menor      - 128/135     - Dó# ou Réb
Segunda maior       - 8/9             - Ré
Terça menor           - 5/6             - Ré# ou Mib
Terça maior            - 4/5             - Mi
Quarta justa            - 3/4             - Fá
Quarta aumentada  - 32/45         - Fá# ou Solb
Quinta justa            - 2/3             - Sol
Sexta menor           - 5/8             - Sol# ou Láb
Sexta maior            - 16/27         - Lá
Sétima menor         - 5/9             - Lá# ou Sib
Sétima maior          - 8/15           - Si
Oitava justa            - 1/2             - Dó (1 oitava acima)

O verdadeiro formato do Sol

     Nosso planeta é esférico com algum achatamento, só que ele é um planeta composto por substancias solidas, já o Sol é composto 81% de hidrogênio, 18% de hélio e 1% de outros elementos, até pouco tempo atrás se imaginava então que o sol tinha um formato extremamente instável e aleatório, porem, recentemente novas descobertas foram feitas!

     Uma bola de aparência incandescente que ilumina os dias, o Sol de fato é o objeto natural mais redondo medido pela ciência. Mas não é na verdade tão esférico quanto parece, conforme vêm mostrando astrônomos. Ele é achatado e menos mutável do que se imaginava, de acordo com artigo publicado no site daScience. “Tivemos acesso a um grande volume de dados que nos renderam medições mais precisas do que as anteriores”, explica o astrônomo Marcelo Emilio, do Observatório Astronômico da Universidade Estadual de Ponta Grossa, no Paraná. Mais do que uma curiosidade sobre a esfera celeste, o formato afeta a órbita dos planetas que gravitam em torno dele.


     O equipamento, a bordo do satélite da agência espacial norte-americana (Nasa) lançado no início de 2010 e batizado como Observador Dinâmico Solar (SDO), capta uma imagem do astro a cada 4 segundos. Além disso, para obter as medidas de achatamento é preciso fazer com que o satélite gire 360° sobre si mesmo, captando imagens solares durante essa rotação. O grupo de Emilio, que inclui pesquisadores da Universidade Stanford, na Califórnia, e da Universidade do Havaí, pôde fazer essa manobra de seis em seis meses. A partir dessas imagens, Emilio considera ter chegado a uma definição do formato do Sol mais precisa do que estava disponível até agora – refinando inclusive trabalho dele próprio publicado em 1997 a partir de dados gerados por outro equipamento da Nasa, o Observatório Solar e Heliosférico (Soho). Tão precisa que detecta um achatamento muito sutil: se o sol fosse uma bola de um metro de diâmetro, seu diâmetro equatorial seria apenas 17 milionésimos do metro maior que o diâmetro polar Norte-Sul. “A grande massa do Sol tende a fazer com que fique redondo, contrariando o achatamento causado pela rotação”, explica o astrônomo.

     Para analisar o interior do Sol, as únicas maneiras são estudar os neutrinos – partículas que são lançadas de lá e em 8 minutos chegam à Terra e a atravessam quase como se ela não existisse, explica Emilio – ou as ondas sísmicas que se propagam como terremotos pelas camadas do Sol, por isso conhecidos como heliomotos. “Agora medimos a parte visível por inteiro”, afirma o pesquisador, que em trabalho anterior estimou o diâmetro do astro em 1.392.684 quilômetros.

     A natureza gasosa do Sol torna sua rotação muito mais complexa que a da Terra, um planeta rochoso. “Não é um corpo rígido, seu equador gira mais depressa que os polos”, detalha. Por isso, trabalhos anteriores postularam que o formato externo varia a cada ciclo solar, que dura 11 anos. Para Emilio e seus colegas, porém, o formato mais simples do Sol – quando se considera os dois polos e o equador – é fixo. Medições posteriores ainda devem definir se há variação em aspectos mais detalhados dessa estrutura geométrica.

     O astrônomo do Paraná estima que as novas medições devem ser bem recebidas pela comunidade especializada, apesar de contradizer hipóteses anteriores, devido ao volume de dados que englobam. Mas não é o fim da história: “Agora o pessoal da teoria vai refinar os modelos existentes”, prevê, se referindo a modelos matemáticos que congregam características como composição química, densidade e tamanho. À medida que mais informações são incorporadas, os pesquisadores alteram os parâmetros do modelo até chegar a um encaixe satisfatório entre teoria e observação. No que diz respeito à publicação, a discussão pode começar depressa: apenas uma semana se passou entre o artigo ser aceito pela Science e publicado em seu site na rubrica ScienceXpress, que disponibiliza publicações antes que saiam na revista impressa.

4 problemas do Infinito

     Nenhum assunto provocou tanta polêmica e tanta discussão entre os matemáticos. O infinito não é um número, não é uma medida: é uma ideia, que representa o que não tem limites ou fim. O conjunto dos números naturais, por exemplo, é infinito, por que não importa qual o número que você tem, sempre poderá adicionar 1 e obter o número subsequente.
     Mesmo sendo a representação de uma ideia, e não um número, o infinito tem algumas propriedades numéricas que permitem que a gente trabalhe com ele. Por exemplo, se representarmos esta ideia com o símbolo ∞, podemos escrever ∞ + 1 = ∞, que pode ser interpretado com “se algo não tem fim, você pode somar 1 e ela ainda será sem fim”.
      A coisa mais importante sobre o infinito é que -∞ < x < ∞, onde x é um número real, que é uma abreviação para a frase "menos infinito é menor que qualquer número real, e infinito é maior que qualquer número real". Algumas operações com o ∞ são indefinidas, como, por exemplo, ∞ + ∞ = ∞, ou - ∞ + - ∞ = ∞. Além disso, existem também os conjuntos com infinitos elementos, e a ideia de tamanhos diferentes de infinitos.
     Mas o mais bizarro são os paradoxos que temos com os números infinitos. Um paradoxo é uma noção verdadeira que desafia nossa intuição, ou até mesmo a lógica. Vejamos alguns paradoxos envolvendo o infinito:

1. Hotel de Hilbert

     Imagine um hotel com infinitos quartos, e que todos eles estão ocupados. Chega um viajante no hotel, e pede para se hospedar. Só que não tem vagas; apesar de ter infinitos quartos, o hotel já está totalmente ocupado.
     Mas o gerente é um sujeito que não manda ninguém embora, e faz o seguinte: pede para o hóspede do quarto 1 se mudar para o quarto 2, o hóspede do quarto 2 se mudar para o quarto 3, o hóspede do quarto 3 se mudar para o quarto 4, e assim por diante.
     E pronto, o hotel que estava cheio, agora tem uma vaga para o novo hóspede. Usando esta estratégia, o gerente do hotel pode acomodar um novo hóspede, 10 novos hóspedes, um milhão de novos hóspedes, ou até um número infinito de novos hóspedes.
     Este paradoxo foi proposto pelo matemático alemão David Hilbert, e é um paradoxo porque a nossa definição de hotel cheio é que não há vagas para novos hóspedes. Mas se o hotel tiver infinitos quartos, mesmo que todos eles estejam cheios, ainda assim dá para acomodar um conjunto de novos hóspedes, até mesmo infinitos novos hóspedes.

2. Trombeta de Gabriel

     A Trombeta de Gabriel, ou a Trombeta do Anjo Gabriel, ou ainda a Trombeta de Torricelli é uma superfície na forma de um funil (ou de trombeta). Ela começa larga e vai afinando rapidamente, mas nunca fica fechada – ou seja, segue até o infinito.
     A superfície da trombeta é infinita, mas o volume que ela envolve não é infinito (uma ideia matemática). Suponha que você tenha que pintar de dourado o lado de dentro desta trombeta. A superfície dela é infinita, então você precisa de uma quantidade infinita de tinta, certo? Bem, você pode pegar uma quantia finita de tinta, correspondendo ao volume da trombeta, e jogar esta tinta na trombeta, deixando ela escorrer.
     Você pode escolher aí o que vai te deixar mais desconfortável: se é uma superfície infinita envolver um volume finito, ou se é uma quantia finita de tinta cobrir uma superfície infinita.
     O discípulo de Galileu; Evangelista Torricelli foi o primeiro a pensar neste problema, que ele achou tão extraordinário que a princípio imaginou que tivesse feito alguma coisa errada.
     Outros filósofos e matemáticos ficaram tão horrorizados com os paradoxos que surgiam com o infinito, que chegaram a propor o banimento da ideia.

3. O enigma do jogo de dardos

     Suponha que você tem um alvo, um dardo, e 100% de certeza que irá acertar o alvo em alguma parte. Agora pense na ponta do dardo, o ponto matemático exato da sua extremidade, e pense em um ponto matemático no alvo. A pergunta é, qual a probabilidade que aquele ponto tem de ser atingido pelo dardo?
     Podemos começar supondo que há uma chance maior que zero daquele ponto ser atingido pelo dardo. Só que aí começam os problemas. Se há uma chance maior que zero de um ponto ser atingido, então há uma chance maior que zero para todos os outros pontos, de que eles serão atingidos pelo dardo. Mas existem infinitos pontos no nosso alvo.
     Se você somar as probabilidades de todos os pontos, vai chegar à conclusão de que o alvo todo tem uma probabilidade infinita de que ser atingido, o que não faz sentido, já que esta probabilidade não pode ser maior que 100%.
     E o que acontece se imaginarmos que a probabilidade de um ponto ser atingido é zero? Se a probabilidade de acertar aquele ponto particular é zero, então ela é zero para todos os outros pontos, e se somarmos as probabilidades de todos os pontos para ter a probabilidade de acertar o alvo, ela é zero. Mas temos certeza de que o alvo será atingido, como pode ser zero, então?

4. Duplicando seu dinheiro

     Imagine que um cassino esteja oferecendo um novo jogo. O jogo começa com um real no banco de apostas. A pessoa joga uma moeda. Se sair cara, o que tem no banco de apostas é dobrado, se sair coroa, o jogo termina e o jogador ganha o que tiver no banco de apostas.
     Quanto você pagaria para entrar neste jogo? Ou quanto seria justo para o cassino cobrar? Se você souber um pouco de matemática já deve ter ouvido falar em “esperança matemática”, ou seja, em um jogo envolvendo probabilidade do ganho esperado. E qual o ganho esperado neste jogo?
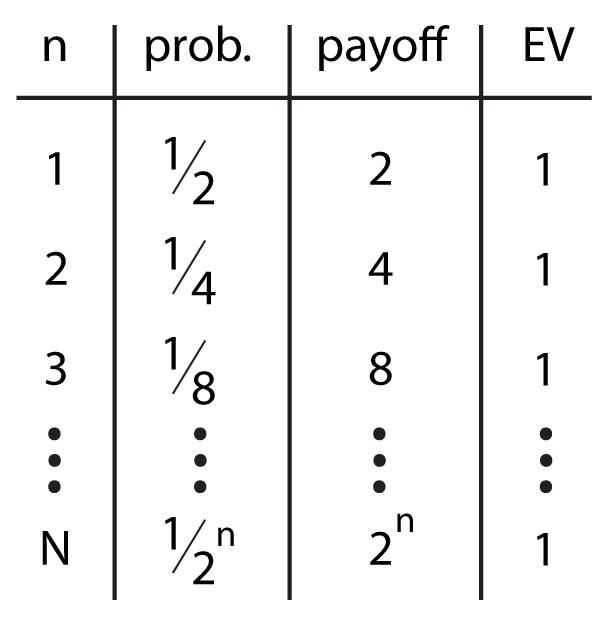
     A maioria provavelmente apostaria R$ 5,00, talvez um pouco mais, mas o que a matemática diz é: “aposte o que você tiver, a esperança de ganho é infinito”. O jogador tem probabilidade de 50% de ganhar R$ 1, 25% de probabilidade de ganhar R$ 2, 12,5% de ganhar R$ 4, e assim por diante. O valor esperado é a soma da probabilidade multiplicada pelo valor do prêmio, assim:
     E = 1/2 + 1/2 + 1/2 + 1/2 + …
     Esta é uma soma de infinitas frações 1/2, e o resultado é infinito. Ou seja, matematicamente falando, a esperança matemática de ganho é infinita. Mas, paradoxalmente, muita pouca gente está disposta a pagar alguma coisa a mais que R$ 20,00 para jogar este jogo.
     Obviamente, estamos falando de um cassino hipotético, capaz de colocar quanto dinheiro for necessário no banco de apostas. Na prática, haverá um limite para o prêmio máximo, e também para o número máximo de jogadas (ninguém vai ficar lançando uma moeda infinitas vezes). Talvez o paradoxo surja daí: ninguém espera ou consegue entender um cassino capaz de cobrir um prêmio infinito ou uma série infinita de caras em uma série infinita de lances de moeda.

Voto Nulo x Branco: A Matemática das Eleições

     Olá eleitores doidinhos. Estamos novamente chegando em época de eleições então resolvi atualizar e publicar novamente esse post. Sempre que se aproxima época de eleições surgem várias dúvidas e discussões sobre esse tema. Espero conseguir neste post tirar algumas dúvidas. Primeiramente quero acabar com a lenda que votos brancos e nulos vão para o candidato que está na frente. Eles favorecem o candidato que está na frente, mas não vai diretamente para ele. Para entendermos melhor, vamos rever a diferença entre votos nulos, brancos e válidos.

     Primeiramente vou dizer aqui que já vi divergência de informações. Dependendo da fonte  consultada diz uma coisa, já em outra fonte diz outra. Então resolvi escolher o próprio TSE, por considerar uma fonte mais segura,  já que é ele quem cria as Leis das Eleições. Segue o link de um boletim informativo do TSE para que consultei para tirar essas dúvidas sobre votos válidos, nulos e brancos. Resumidamente a parada é assim, votos válidos é qualquer voto nominal a um candidato regularizado no TSE, ou o voto na legenda do partido. Voto nulo é aquele voto que vai para um candidato inexistente, ou por este estar indevidamente registrado no TSE, ou por ter digitado número incorreto na urna (ou na época da cédula, quando fazia um quadrado a mais e votava no Darth Vader, tempo bom esse....) e voto em branco é aquele voto que não vai pra nenhum candidato. Votos nulos e em branco não são considerado como votos válidos, portanto não entram na contabilidade eleitoral, então eles não vão diretamente para o candidato que está na frente.
     Mas embora esses votos nulos e brancos não entram na contagem de votos, eles acabam favorecendo este candidato da frente, mas como? Eles favorecem pois alteram o número total de votos contabilizados, e como um candidato  para ser eleito precisar ter a maioria dos votos válidos, eles ajudam modificando essa porcentagem. Para ficar mais fácil de entender vamos visualizar o seguinte cenário: uma eleição com 100 eleitores. imaginem que 49 dos eleitores votem no candidato A, ele tem 49% do total de votos. Se todos os 100 votos fossem válidos, o candidato A não seria eleito no primeiro turno, obrigando a todos nós perder mais um domingo indo às urnas. Porém se o candidato A obter os mesmo 49 votos, mas houver 10 votos nulos/brancos, a contabilização dos votos válidos será 90 votos. Então o candidato A terá 49/90x100 = 54% dos votos válidos, assim ganhando a eleição em primeiro turno. Simples assim.
     Bom, espero que tenha entendido, e que nesta eleição acompanhem os debates dos candidatos, saibam quais são suas propostas de governo, pesquisem sobre o passado dos candidatos (em fontes confiáveis) para saber quais candidatos costumam cumprir as promessas, e acima de tudo votem com consciência. Lembrem-se que apesar das diferenças políticas somos todos irmãos, então sem brigas!!!

O Último Teorema de Fermat, de Simon Singh

     Bom pessoal. Hoje irei falar de um livro que li um tempo atrás. O Último Teorema de Fermat, de Simon Singh, que conta a história do problema matemático mais difícil do mundo, um enigma praticamente insolúvel que desafiou as maiores mentes por cerca de 358 anos. Novamente, assim como outros livro que já escrevi aqui, embora tema parecer ser assustador para a maioria das pessoas, não precisa ser um expert em matemática para lê-lo. O autor consegue abordar o assunto de uma maneira bem simples e não técnica, bastante acessível ao público leigo, contando as histórias das vidas de grandes matemáticos do mundo. O livro trata da história das idéias, desenvolvimento e soluções de problemas, uma saga de coragem, fraudes, astúcias e tragédias, uma busca épica para resolver o maior problema de matemática de todos os tempos.
     Pierre de Fermat nasceu em 17 de agosto de 1601, na cidade de Beaumont-de-Lomages na França, filho de um rico mercador teve uma educação privilegiada. Estudou inicialmente no mosteiro franciscano de Grandselve, e posteriormente formou-se em Direito na Universidade de Toulouse. Foi advogado e oficial do governo de Toulouse durante maior parte de sua vida. Considerado como "Principe dos Amadores" nunca teve formalmente a matemática como atividade principal de sua vida. Jurista e magistrado por profissão, dedicava à Matemática apenas em suas horas de lazer, e mesmo assim, foi considerado por Blaise Pascal como o maior Matemático de seu tempo. Em 1636 Fermat propôs um sistema de Geometria Analítica, semelhante aquele que Descartes proporia anos depois. As contribuições e Fermat para o cálculo geométrico e infinitesimal foram inestimáveis. Contudo o ramo que mais interessava a Fermat era Teoria dos Números, que tem poucas aplicações práticas claras. E foi nesse ramo que enunciou seu famoso teorema, conhecido como O Último Teorema de Fermat.
     "Eu descobri uma demonstração maravilhosa, mas a margem deste papel é muito estreita para contê-la." Com esta anotação incompleta, feita em 1637, o matemático francês Pierre de Fermat, que morreu antes de demonstrar seu teorema, lançava o desafio que iria confundir e frustrar os matemáticos mais brilhantes do mundo. O teorema tem um enunciado bastante simples: Não existe conjunto de números inteiros positivos x, y, z e n, com n maior que 2 que satisfaz a equação . Fermat escreveu este teorema nas margens do seu livro Aritmética, de Diofante, seguido da frase que dizia que ele tinha a demonstração para provar que o teorema era verdade, mas a margem do livro era pequena demais para escrever nela (aliás, escrever em margens dos livros era um costume de Fermat). Para n=2 existe várias soluções, como aprendemos no famoso Teorema de Pitágoras qualquer triângulo retângulo tem os lados x² + y² = z², mas para n>2 e brincadeira complica um pouco. Para provar que existe uma solução, basta apresentar uma das soluções possível, mas provar que "não existe solução" é necessário mostrar que todos valores infinitos de x, y, z e n não satisfazem a equação. Não se sabe se Fermat realmente tinha uma demonstração que provasse que não existia nenhum resultado possível, ou se foi a maior trollada da história da matemática.
    O Último Teorema de Fermat, como ficou conhecido, tornou-se o santo graal da matemática. As maiores mentes da matemática devotaram e sacrificaram suas vidas em busca de uma demonstração para um problema aparentemente simples. O maior matemático do séc. 18, Leonhard Euller, teve que admitir sua derrota. Atrás de uma solução, Sophie Germain assumiu a identidade de um homem para poder  pesquisar num campo que era restrito aos homens, e fez a descobera mais significativa do séc. 19. O jovem gênio Évariste Galois (cuja trágica história já foi contada aqui num post sobre o livro A Equação que Ninguém Conseguia Resolver) passou a noite escrevendo os resultados de sua pesquisa, antes de morrer em um duelo em 1832.  O empresário Paul Wolfskehl afirmava que Fermat o salvara do suicídio e criou um valioso prêmio para primeira pessoa que demonstrasse o teorema. Por outro lado, o gênio Yutaka Taniyama, cujas descobertas levaram à solução do enigma, matou-se em 1958. E  o matemático Andrew Wiles conseguiu finalmente demonstrar em 1995, utilizando as mais modernas ferramentas matemáticas disponíveis da atualidade em 100 páginas de cálculos, incluindo a teoria dos grupos de Galois, o método de  Kolyvagin-Flach e tendo por base a conjectura Taniyama-Shimura (feita pelos matemáticos Yutaka Taniyama e Goro Shimura na década de 1950). Alguns matemáticos mais românticos acreditam que Fermat teria uma prova genuína. O que quer que tenha sido esta prova,  ela teria sido baseada na matemática do séc. 17 e teria um argumento tão astucioso que escapou a todos, de Euler a Wiles.

A História dos Foguetes - Corrida Espacial

    A corrida espacial foi uma das fases mais bacanas da história moderna. Em plena guerra fria as duas super-potências mundias brigavam pela ver quem chegava primeiro à Lua. E ela quase foi Vermelha. Mas por trás da disputa da Lua, os interesses eram muitos maiores. A corrida espacial teve origem na corrida armamentista iniciada após a segunda guerra mundial, entre Estados Unidos e União Soviética. Foi uma disputa pela supremacia da tecnologia da exploração espacial, oque significava espiar inimigos com satélites e foguetes para para mandar bomba atômica. Porém a tecnologia e ciência necessária para leva o homem a Lua começou bem antes.

     Entre as várias tecnologias necessárias, a principal é a tecnologia dos foguetes. O primeiro combustível sólido para foguetes era uma espécie de pólvora. A pólvora foi descoberta na china,durante a dinastia Han, acidentalmente por alquimistas taoistas que procuravam o elixir da longa vida, produziram vários incêndios ao fazer testes com enxofre e salitre (nitrato de potássio). As primeiras referências aparecem em textos como avisos para não misturarem certos materiais com outros. No séc. VIII, ao final da dinastia Tang, foi descoberta a fórmula para fazer a pólvora. Inicialmente usado para fogos de artifícios, a pólvora começou com propósito militares a partir do séc. X na china, como foguetes e bombas explosivas lançadas por catapulta. A primeira referência a canhão surge em 1126, usando tubos de bambu para lançar foguetes contra os inimigos. Após, o bambu foi substituído por tubos de metal. Da china, o uso militar da pólvora foi difundido para o Japão e Europa. A pólvora foi usada pela primeira vez para lançar projéteis de uma arma portátil semelhante à um rifle em 1304. A pólvora clássica (explosiva) é composta de 75% de salitre, 15% de carvão e 10% de enxofre. Ao longo dos séculos, a composição da pólvora foi modificada, dependendo da utilização, surgindo as pólvoras de caça, de minas e de guerra. A pólvora pode ser dividida em duas categorias: propelente, de combustão lenta e controlada; e explosiva, de combustão rápida e explode se confinada.

     Nesse ponto da história aparecem os primeiros foguetes primitivos. Os documentos chineses registram o uso de "setas de fogo", apenas uma seta com propulsão usadas para repelir invasores mongóis na batalha de Kai-fung-fu em 1232 d.C. Nos séculos que se seguiram, esses foguetes foram espalhado pelos resto do mundo, sofrendo algumas alterações e melhoramentos. Na parte teórica, o primeiro passo importante foi dado em 1687, quando Isaac Newton publicou sua obra-prima Princípios Matemáticos da Filosofia Natural, anunciando a famosa e temida (pelos estudantes) Lei da Gravitação Universal, usada para calcular a trajetórias de todos os corpos sob ação da gravidade, sendo essencial para levar o Homem a Lua. A partir de então começou-se a pensar em usar essa tecnologia para sair da Terra. Em seus primórdios a Astronáutica era puramente teórica. Muito antes de ser possível enviar foguetes ao espaço, o voo espacial maravilhou muitas das mentes do séc. XIX, como Julio Verne e HG Wells. Mas os primeiros passos para a Astronáutica moderna só seriam dados no séc. XX.

Tsiolkovsky

     O próximo passo na parte teórica da astronáutica foi dado pelo professor e cientista russo Konstantin Eduardovich Tsiolkovsky. Caso se lembrem (se é que alguém lê este blog), já falei brevemente dele no post sobre Selos Postais que homenageiam grandes Equações Matemáticas. Nascido em Izhevskoye, no território do Império Russo, no ano de 1857, Tsiolkovsky foi um pioneiro no estudo dos foguetes e cosmonáutica (não há diferença entre a cosmonáutica e astronáutica, apenas os russos adotaram o primeiro termo e os EUA adotaram o segundo). Durante a infância, Konstantin sofreu um infecção no ouvido reduzindo suas capacidades auditivas. Não sendo aceito nas escolas primárias por esse problema auditivo, ele recebeu educação em casa até os 16 anos. Quase surdo, trabalhou como professor de matemática do ensino secundário até a reforma em 1920. Tsiolkovsky estabeleceu as fundações teórica para muitos aspectos da propulsão de foguetes e viagem espacial. Em 1903 publicou o primeiro estudo acadêmico sobre foguetes, chamado "A exploração do espaço cósmico por meio de dispositivos de reação", baseando-se na Terceira Lei de Newton, conhecida como Lei da Ação e Reação. Ele também foi o primeiro a calcular que a velocidade de escape (velocidade necessária para escapar da gravidade da Terra) para a órbita era de 8 km/s e para atingir essa era necessário um foguete de múltiplo estágios utilizando oxigênio líquido e hidrogênio líquido como propelentes. Durante vida ele publicou mais de 500 obras, sobre viagens espaciais e histórias de ficção científica. Tsiolkovsky também estudou sobre aviação, efetuando independentemente muitos dos cálculos que Santos Dummont efetuou na mesma época, porém ele nunca construiu modelos práticos. Ele foi um grande teórico, porém suas idéias permaneceram desconhecidas fora da rússia por um tempo. Com sua famosa equação de foguetes tornou-se possível calcular a velocidade final do foguete v em função da massa final do foguete m0 (sem propelente), sobre sua massa inicial m1 (foguete + propelente) e a velocidade de exaustão do propelente ve:

Goddard e seu foguete de 1926

     Agora que já se tinha a base teórica para os foguetes modernos, o próximo passo seria dado no campo prático. E quem deu esse passo foi um seguidor de Tsiolkovsky, o físico experimental Robert Goddard, nascido em 1882. Quando criança ficou fascinado pelo foguetes e efeitos pirotécnicos em festas, e desde então ficou imaginando como se poderia aproveitar aquela energia para por objetos a voar. Goddard estudou no Instituto Politécnico de Worcester e na Clark University, onde se especializou em física. Seus estudos sobre foguetes o levou a provar que eles poderiam viajar no vácuo, recorrendo às leis da ação e reação. Em 1919 publicou um livro chamado "Um Método para alcançar Altitudes Extremas" onde descrevia um foguete capaz a alcançar a lua. Quatro anos depois iniciou os primeiros testes de motores de foguetes usando combustível líquido. Em 1926 lançou o primeiro foguete usando como combustível uma mistura de petróleo e oxigênio líquido. Esse teste foi realizado no quintal de uma tia de Goddard, e o foguete atingiu uma altura de 12,5 metros. O voo durou 2,5 segundos e caiu a uma distância de 56 metros em cima de uma barraca abandonada. Em seus próximos foguetes ele foi aperfeiçoando as técnicas de propulsão e estabilidade, além de adicionar instrumentos como barômetro, termômetro e câmera de filmar. Entre 1930 e 1942, Goddard trabalhou em Roswell, no estado do Novo México. Durante esse período ele registrou 200 patentes sobre engenharia de foguetes. Ao final dessa época seus foguetes já tinham evoluídos a tal ponto que atingiam a velocidade de 885 K/h e 2 quilômetros de altura. Os foguetes de Goddard eram pequenos em comparação aos modernos, mas já tinham todos os princípios dos foguetes modernos, como orientação por giroscópio.
     Bom, saindo um pouco da parte histórica, quero falar um pouco da prática. O princípio básico do funcionamento de foguetes é a Propulsão, que é o movimento criado a partir da força que dá o impulso, seguindo o princípio da Lei da Ação e Reação. Como propulsão, os motores baseiam-se em uma reação química de combustão rápida, mas não explosiva, com alto desenvolvimento de alto volume de gases de combustão. Como vimos no início, primeiramente foi usado combustível sólido, mas depois perceberam que o combustível líquido era mais eficiente, embora atualmente ainda se usa combustível sólido para alguns casos. Na figura à esquerda, o aspecto básico de um motor mostrando a progressão de queima do combustível com o tempo. Na direita a Câmara de Combustão, que contém o combustível, e na esquerda a Tubeira, corpo convergente-divergente que canaliza os gases para a saída. O princípio de funcionamento baseia-se na liberação dos gases, que darão uma alta pressão na câmara de combustão, saindo depois pela tubeira em alta velocidade. A tubeira é uma parte essencial, desenhada de modo que o escoamento de gases para o exterior provoque o maior impulso possível. O escape dos gases provoca, por ação/reação, uma força sentido contrário ao escoamento, e é essa força F que é responsável pelo movimento do foguete.
     Embora trabalho Goddard não tivesse sido imediatamente reconhecido nos Estados Unidos, os alemães aproveitaram suas pesquisas para dar o próximo passo, e desenvolveram as primeiras armas baseadas na engenharia de foguetes: os terríveis mísseis V-2. A paritr daí essa corrida começa a ficar cada vez mais maneira, mas irei deixar para contar na segunda parte do post.

Os Caçadores de Vênus - Livro

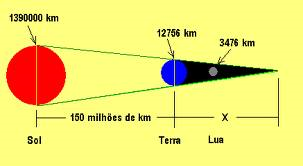
     Olá pessoal. Hoje irei falar um pouco de um dos melhores livro que li ano passado, Os Caçadores de Vênus, da escritora e historiadora Andrea Wulf. Em 1687, Isaac Newton revolucionou o mundo ao publicar a sua obra-prima Princípios Matemáticos da Filosofia Natural, e logo após cientistas do mundo inteiro começaram a aplicar os princípios de gravidade e movimento para prever os movimentos dos corpos celestes. O primeiro deles foi o astrônomo e matemático britânico Edmond Halley (sim, o do cometa), que teorizou que os cometas seriam corpos periódicos, e em 1696 previu que o cometa Halley (na época ainda não era chamado assim) voltaria a ser visto em 1758 (e acertou em cheio). Em 1716 ele mostrou como a distância entre Terra e Sol poderia ser calculada através da passagem de Vênus entre o Sol e a Terra. Esse evento ocorreria em 1761 e, em seguida, em 1769. Após isso passariam mais de cem anos para que ocorresse novamente. Halley, nascido em 1656, provavelmente não estaria vivo para ver o transito de Vênus (1761-69), então ele publicou um ensaio de 10 páginas em que conclamava os cientistas a se reunirem num projeto que abarcaria todo o planeta, e que poderia modificar o mundo da ciência para sempre. E é essa a história desse livro, o primeiro Grande Empreendimento Cientifico.
     Como as órbitas de Vênus e da Terra possuem inclinações diferentes, Vênus normalmente aparece acima ou abaixo do Sol (e portanto não pode ser visto da Terra). Halley previu que no dia 6 de junho de 1761 Vênus passaria na frente do Sol, e durante algumas horas a estrela brilhante apareceria como um círculo negro perfeito. Ele acreditava que, medindo o tempo exato e a duração desse raro encontro celeste, os astrônomos poderiam obter dados necessários para calcular a distância entre a Terra e o Sol. Halley explicou que era essencial que diversas pessoas em lugares diferentes, em todo mundo, medissem o raro encontro ao mesmo tempo. Não bastava ver a passagem de Vênus apenas na Europa, os astrônomos precisariam viajar a lugares remotos, tanto no hemisfério norte quanto no sul, e somente se eles combinassem esses resultados poderiam alcançar uma compreensão matemática precisa do sistema solar.
     Então no dia 30 de abril de 1760, o astrônomo oficial da Marinha Francesa Joseph-Nicolas Deslile digiriu-se a uma reunião da Academie des Sciences, em Paris. A partir desse encontro, eles teriam pouco mais de 1 ano para organizar as viagens de 12 cientistas ao redor do globo que enfrentarão tempestades, terremotos, doenças e até a morte para realizar a Maior Expedição Científica realizada até então.
     O livro é divido em 2 partes, o trânsito de 1761 e o trânsito de 1769, e conta relatos das aventuras dos cientistas que viajaram aos lugares mais distantes do globo para poder registrar esse raro evento astronômico. Baseado em diários de bordo, registros científicos e relatos históricos, de um tempo em que fazer ciência era uma aventura a la Indiana Jones, um tempo onde homens embarcavam em viagens ao desconhecido.
     Esse não é um livro só sobre astronomia, é um livro sobre aventuras, descobertas e amor pela ciência. De leitura fácil irá agradar qualquer pessoa que tiver curiosidade suficiente para dar uma chance a ele. Recomendo!

"Devemos mostrar que somos melhores, e que a ciência fez mais pela humanidade do que a Graça suficiente ou Divina."

                                                                                                    Denis Diderot

Quer que Desenhe? - A Gravidade

Olá pessoal. Após um breve momento de inatividade estou de volta. :)

Vi esse vídeo muito bom da série Quer que Desenhe? de Carlos Ruas (do site Um Sábado Qualquer) e resolvi compartilhar aqui com vocês.

Nesse vídeo ele aborda o tema Gravide (não a m&$#@ de filme) que é um tema bem complexo, porém ele consegue abordar com muita simplicidade.

Eu gostaria de fazer apenas uma observação em relação ao vídeo, um pequeno detalhe: quando ele diz que Einstein descobriu "a verdadeira natureza da gravidade", temos que ter muito cuidado pois uma teoria científica é apenas uma descrição da natureza, sendo "verdadeira" em apenas alguns casos específicos, e tem sua aplicabilidade limitada à alguns casos e épocas. Por isso sempre que alguma teoria cai em desuso aparece uma teoria nova para descrever a natureza estudada.
Portanto não podemos dizer que Newton estava errado e nem que a teoria de Einstein representa a Verdadeira natureza da Realidade. Os dois estavam corretos em suas limitadas aplicabilidades e são apenas teorias que descrevem a natureza, mas não são a verdadeira realidade. Aliás, já fiz um post sobre O que é Realidade???, que é uma parte de um capítulo do livro chamado O Grande Projeto , do Stephen Hawking e Leonard Mlodinow, que aborda genialmente essa discussão.
Há, também gostaria de salientar que a história da maçã que caí na cabeça de Newton provavelmente é apócrifa.
Até mais pironautas.